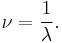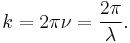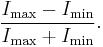Spatial frequency

In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier transform) of the structure repeat per unit of distance. The SI unit of spatial frequency is cycles per meter. In image processing applications, spatial frequency is often expressed in units of cycles per millimeter and sometimes incorrectly in units of line pairs per millimeter (incorrect since a line pair may describe a square wave but not a sinusoidal wave).

In wave mechanics, the spatial frequency \nu is related to the wavelength \lambda by the formula

\nu = \frac{1}{\lambda}.

Likewise, the wave number k is related to spatial frequency and wavelength by

k = 2 \pi \nu = \frac{2 \pi}{\lambda}.

Contents

Visual perception

In the study of visual perception, sinusoidal gratings (images containing bands of white and black in a regular pattern) are frequently used to probe the capabilities of the visual system. In these stimuli, spatial frequency is expressed as the number of cycles per degree of visual angle.

Different spatial frequencies convey different information about the appearance of a stimulus. High spatial frequencies represent abrupt spatial changes in the image, such as edges, and generally correspond to configural information and fine detail. Low spatial frequencies, on the other hand, represent global information about the shape, such as general orientation and proportions.[1] In the general population of adults, the threshold for spatial frequency discrimination is about 7%. It is often poorer in dyslexic individuals.[2]

Sinusoidal gratings and Michelson equation

There is an important quantitative concept related to spatial frequency, known as the Michelson equation:

\frac{I_\mathrm{max}-I_\mathrm{min}}{I_\mathrm{max}%2BI_\mathrm{min}}.

In layman's terms, this is the ratio of the crest-trough distance to the maximum thereof, which is twice the average. One degree on the visual field represents four cycles on the wave pattern.[3]

See also

References

  1. ^ Bar M (Aug 2004). "Visual objects in context". Nat. Rev. Neurosci. 5 (8): 617–29. doi:10.1038/nrn1476. PMID 15263892. "
    Box 2: Spatial frequencies and the information they convey"     
  2. ^ Ben-Yehudah G, Ahissar M (May 2004). "Sequential spatial frequency discrimination is consistently impaired among adult dyslexics". Vision Res. 44 (10): 1047–63. doi:10.1016/j.visres.2003.12.001. PMID 15031099. 
  3. ^ "Vision" McGraw-Hill Encyclopedia of Science & Technology, vol. 19, p.292 1997

External links